Pour prédire le passage d’un satellite à un endroit donné, on a besoin de connaître comment est décrit son orbite. Pour cela, on va utiliser un standard qui se nomme TLE se basant sur 6 paramètres physiques.

TLE (paramètres orbitaux à deux lignes)

Pour savoir quand est-ce que va passer un satellite au dessus de nous, on peut utiliser SatDump, N2YO ou bien d’autres. Mais tous ont en commun de se baser sur les mêmes données, à savoir les TLE (Two Lines Elements) qui sont propre à chaque objet en orbite autour de la Terre. La NASA et la NORAD les calculent régulièrement (car les orbites des objets changent) puis les publient sur des bases de données comme CelesTrak sur lesquelles se base nos fameux outils de prédiction.
Prenons le TLE de NOAA 19 à date où j’écris l’article en guise d’exemple :

NOAA 19
1 33591U 09005A   24285.49466946  .00000972  00000-0  54355-3 0  9997
2 33591  99.0340 342.4576 0013141 327.7681  32.2687 14.13153634808053

La deuxième ligne est celle qui nous intéresse car c’est grâce à elle qu’on détermine à quoi ressemble l’orbite de l’objet en question. Et pour les plus courageux, c’est sur ces mots barbares qu’on va poursuivre le cours en s’aidant du super site Orbital Mechanics.

L’inclinaison

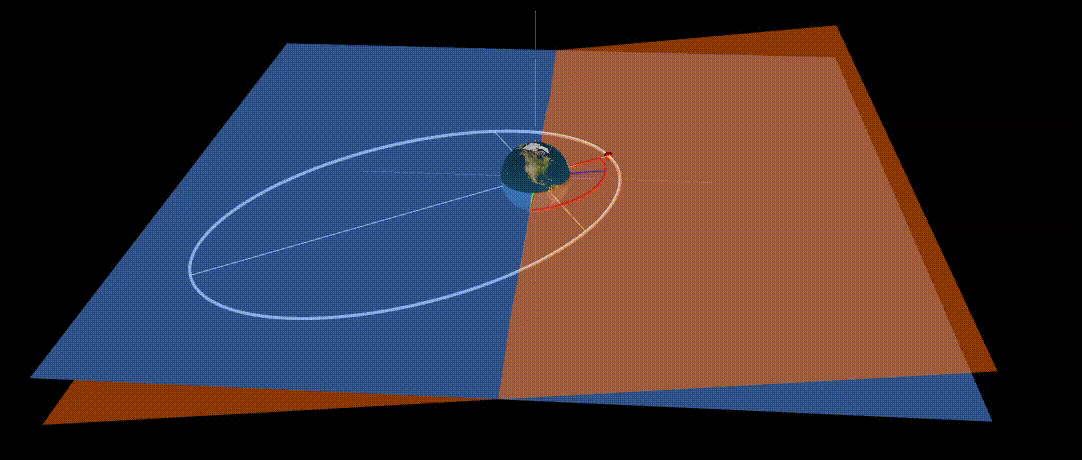
Noté i, c’est l’angle d’inclinaison en ° du plan de l’orbite par rapport au plan équatorial.
En bleu, c’est le plan de l’orbite terrestre. En orange, c’est le plan de l’orbite du satellite.

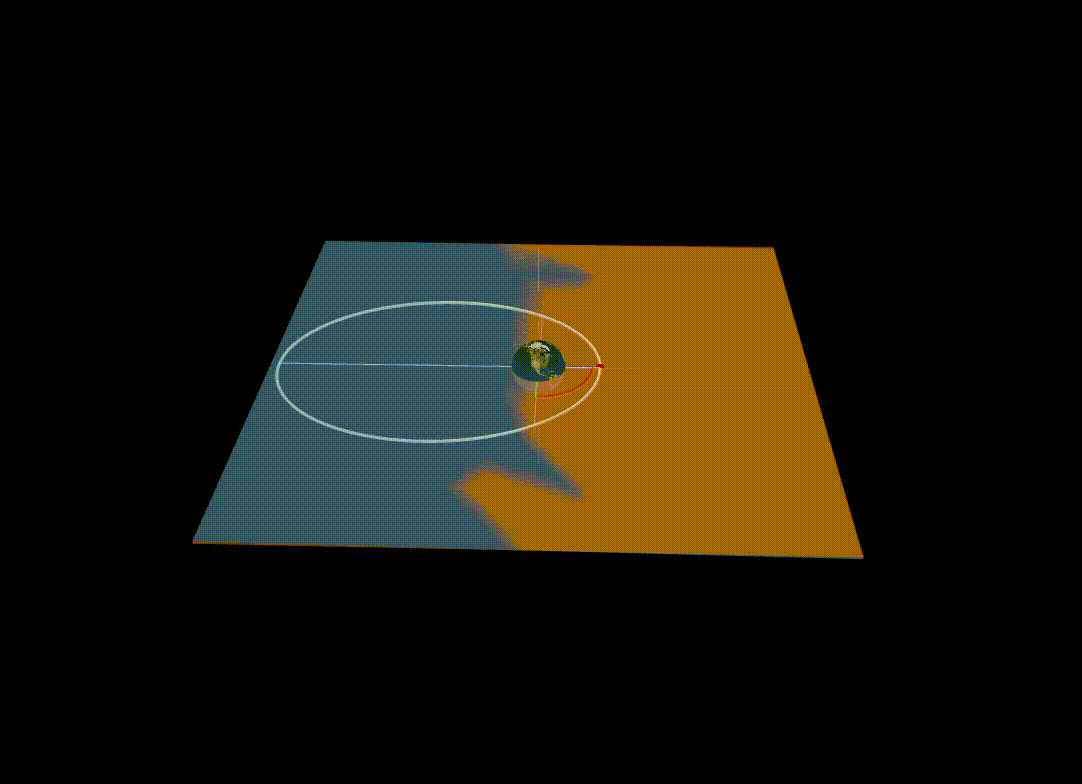
On distingue 3 types d’inclinaison :

• 0°≤i≤90° : Prograde, le sens de l’orbite est le même que le sens de rotation de la Terre (ouest vers l’est).
• 90°<i≤180° : Rétrograde, le sens de l’orbite est à l’inverse du sens de rotation de la Terre (est vers l’ouest).
• i=90° : Orbite polaire, cas particulier qui couvre toutes les latitudes.

Longitude du nœud ascendant

Noté Ω, c’est l’angle entre le nœud ascendant et le point vernal. J’avoue, ça n’aide pas 😄.

Nœud ascendant

D’abord, la notion de nœud ascendant et tant qu’on y est de nœud descendant :

Le nœud ascendant, c’est le croisement entre le plan de l’orbite terrestre et celle du satellite lorsque ce dernier “remonte”. Le nœud descendant, c’est pareil mais inversement.

Point Vernal

Le point vernal, c’est en gros le nœud ascendant de l’orbite du Soleil avec celle de la Terre.
L’écliptique, c’est l’orbite que décrit le Soleil autour de la Terre. L’équateur céleste, c’est le plan défini par l’équateur terrestre.

Longitude du nœud ascendant

On comprend (à peu près) mieux la première phrase : La longitude du nœud ascendant, c’est l’angle entre le nœud ascendant et le point vernal.

Bon, j’avoue, c’est le plus dur de tous à assimiler mais voyons ce que si passe quand on change cet angle avec orbital Mechanics :

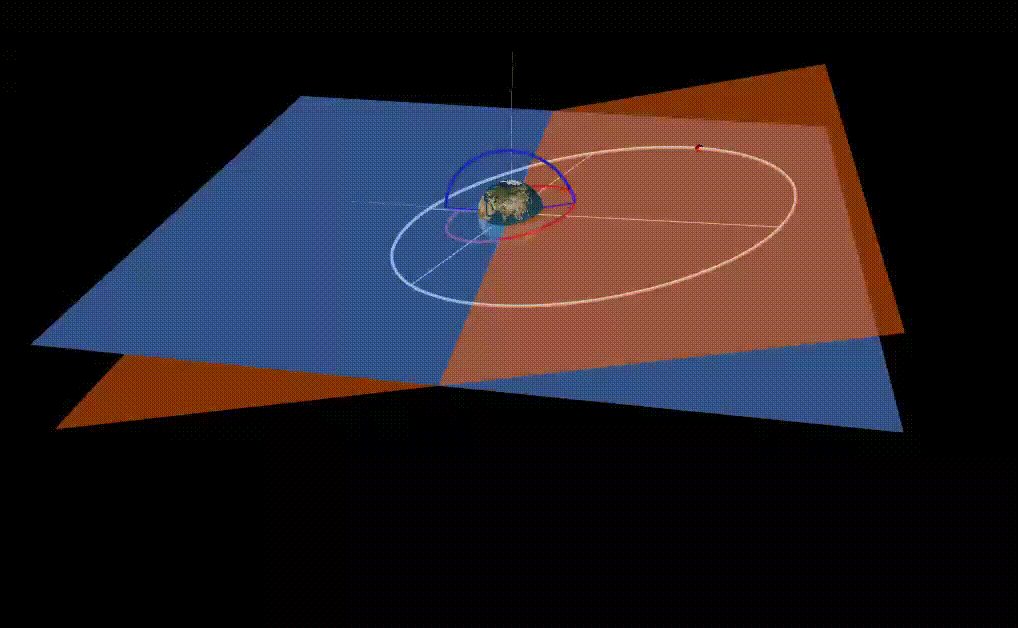
Le demi-grand axe

Bien que non présent dans les TLE, ce paramètre est à prendre en compte pour la représentation d’une orbite.

Noté a, il représente la moitié du grand axe d’une ellipse.
Voilà comment se modifie notre orbite lorsque que l’on modifie cette valeur :

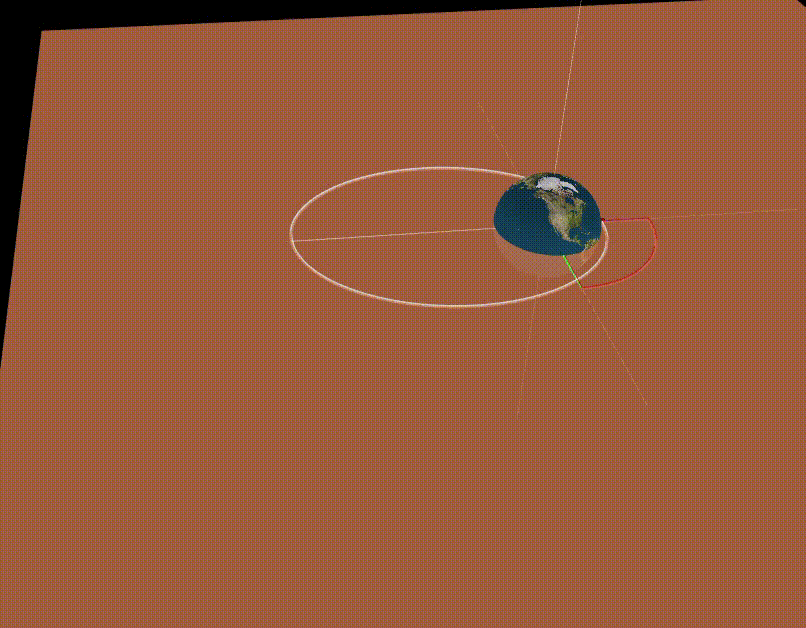
L’excentricité

Noté e, ça représente l’aplatissement d’une ellipse. Elle se calcule à partir des longueurs du demi-grand axe a et du demi-petit axe b avec cette formule.
Pour e=0, on a un cercle parfait (orbite & chemin fermé).
Pour 0<e<1, on a une ellipse (orbite & chemin fermé). C’est ce type d’excentricité qu’on aura affaire pour les satellites.
Pour e=1, on a une parabole (trajectoire ouverte).
Pour e>1, on a une hyperbole (trajectoire ouverte).

Changement de e :

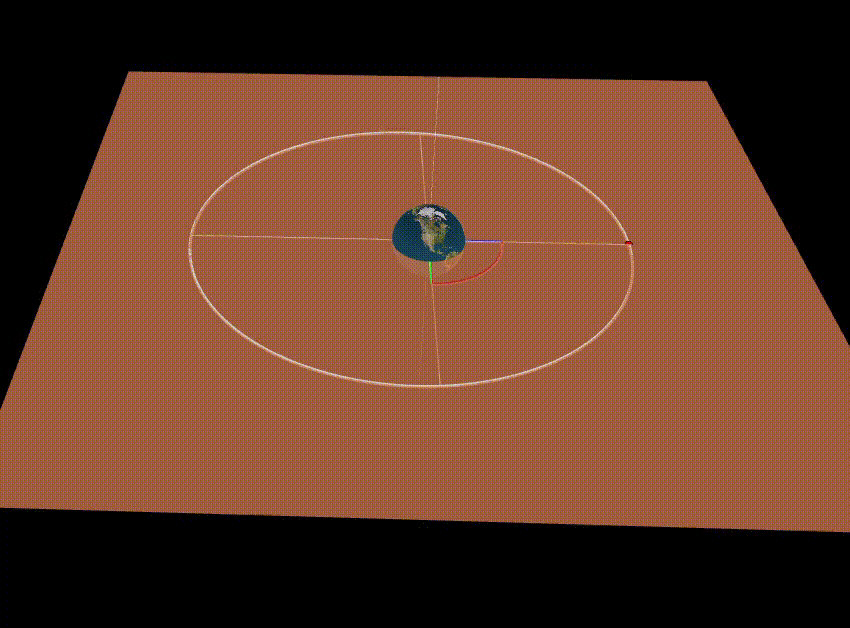
L’argument du Périastre

Noté ω, c’est l’angle en ° entre le nœud ascendant et le périastre.

Le périastre, c’est le point sur l’orbite où le satellite est au plus proche de l’astre autour duquel il tourne.
Si l’astre c’est la Terre, on parle de périgée et d’apogée (périhélie et aphélie pour le Soleil).
Voyons ce qui se passe quand on change cet valeur :

L’anomalie vraie

Noté 𝜈, c’est l’angle en ° entre le périastre d’une orbite et la position actuelle du satellite. En fait, c’est ce paramètre qui nous permet de situer le satellite sur notre orbite. Sur le schéma ci-dessous, en fonction de l’angle, le satellite sera à différents endroits sur l’orbite.

Donc voilà, on a :

• La taille et la forme de notre orbite grâce au demi-grand axe et l’excentricité.
• L’orientation de l’orbite grâce à l’inclinaison, la longitude du nœud ascendant et l’argument du périastre.
• La position du satellite grâce à l’anomalie vraie.

Et c’est bon, on a réussi à arriver jusqu’au bout, BRAVO 😎.
Retenez surtout qu’on va souvent utiliser les TLE car c’est grâce à eux qu’on pourra prédire le passage d’un satellite à un endroit bien précis.
Pour ceux qui auraient besoin d’une autre représentation visuelle, y a cette super vidéo.